感谢清华NLP组GitHub仓库，让我不用一篇篇找图神经网络的论文，为了加深理解，顺便也为blog里多些内容，我决定写一点阅读笔记放在这。理解浅显，还望指教。

目录

first book

开头先看综述类，涨涨见识。第一类的第一本就是清华NLP刘知远老师的书Introduction to Graph Neural Networks（不禁让我怀疑这是作者的私心）。这本书貌似需要资源，所以我果断前往sci-hub(大家不要学我)。

目录结构

纵览全书，本书对图神经网络的介绍可以分为以下几个模块：

  1. 背景介绍
  2. 朴素图神经网络
  3. 图卷积神经网络
  4. 图循环神经网络
  5. 图注意力网络
  6. 图残差网络
  7. 针对不同类型的图的变种模型和高级训练方式的变种
  8. 模型之外的东西：应用、资源and so on

我主要阅读对于不同图神经网络模型的介绍，结合一些他人的博客与分享，希望能够建立一个大概的蓝图框架。

朴素图神经网络

$$ h_v=f(x_v,x_{co[v]},h_{ne[v]},x_{ne[v]})(1)\\ o_v=g(h_v,x_v)(2) $$

对于顶点$v$，它的隐藏state（hidden state）由顶点v的属性$x_v$ 和邻接边的特征 $x_{co[v]}$、邻居节点的隐藏状态$h_{ne[v]}$、邻居节点的属性所共同决定，而它的输出则由上面计算出的隐藏状态$h_v$和顶点v的属性$x_v$所决定。其中$f$是local transition function，$g$是local output function。

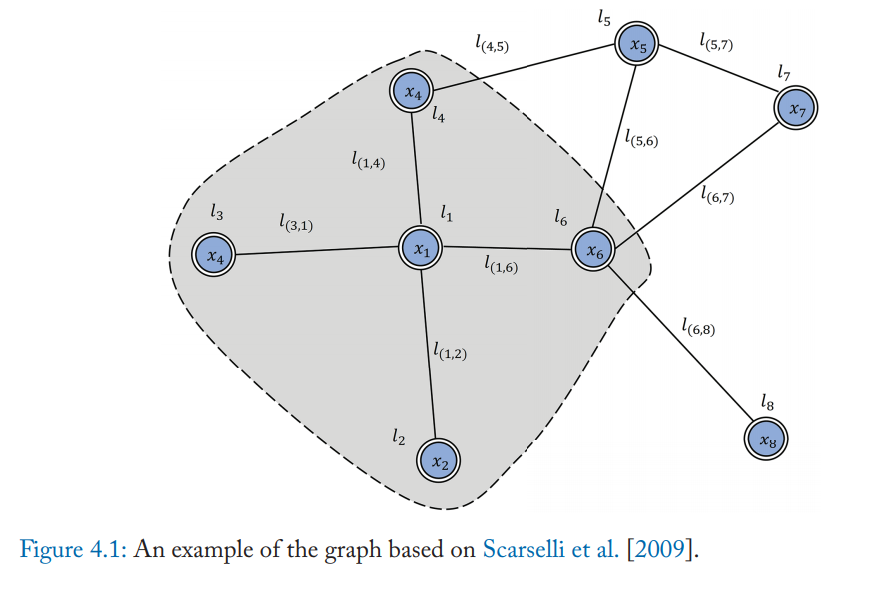
image-20210601121646373

损失函数： $$ loss=\sum_{i=1}^p(t_i-o_i) $$ $t_i$是顶点i的target。

使用$(1)$式不断更新h，直到h几乎不变(逼近固定点Banach’s fixed point theorem)，再用loss function更新权重的梯度。

图卷积神经网络

图卷积神经网络可以大体分为两类：

  1. 基于频域的卷积
  2. 基于空域的卷积

参考https://www.cnblogs.com/SivilTaram/p/graph_neural_network_2.html

频域有坚实的理论基础，空域有更直观的概念（目前应用的人似乎也更多些）。“通俗点解释，空域可以类比到直接在图片的像素点上进行卷积，而频域可以类比到对图片进行傅里叶变换后，再进行卷积。”

“基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上，它跟传统的卷积神经网络中的卷积更相似一些。在这个类别中比较有代表性的方法有 Message Passing Neural Networks(MPNN)[1], GraphSage[2], Diffusion Convolution Neural Networks(DCNN)[3], PATCHY-SAN[4]等。

基于频域卷积的方法则从图信号处理起家，包括 Spectral CNN[5], Cheybyshev Spectral CNN(ChebNet)[6], 和 First order of ChebNet(1stChebNet)[7]等。”

空域卷积(Spatial Convolution)

介绍完卷积的基础概念后，我们先来介绍下空域卷积(Spatial Convolution)。从设计理念上看，空域卷积与深度学习中的卷积的应用方式类似，其核心在于聚合邻居结点的信息。比如说，一种最简单的无参卷积方式可以是：将所有直连邻居结点的隐藏状态加和，来更新当前结点的隐藏状态。

频域卷积(Spectral Convolution)

空域卷积非常直观地借鉴了图像里的卷积操作，但据笔者的了解，它缺乏一定的理论基础。而频域卷积则不同，相比于空域卷积而言，它主要利用的是图傅里叶变换(Graph Fourier Transform)实现卷积。简单来讲，它利用图的拉普拉斯矩阵(Laplacian matrix)导出其频域上的的拉普拉斯算子，再类比频域上的欧式空间中的卷积，导出图卷积的公式。

恒等式$(f∗g)(t)=F−1[F[f(t)]⊙F[g(t)]]$

频域卷积

Spectral Network

Bruna et al. [2014] $$ g_{\theta}\star x=Ug_{\theta}(\Lambda)U^Tx $$ $U$是归一化图拉普拉斯算子的特征向量矩阵，$L=I_N-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=U\Lambda U^T$,$D$是度矩阵，$A$是邻接矩阵

第一代的参数方法存在着一些弊端，主要在于： （1）计算复杂：如果一个样本一个图，那么每个样本都需要进行图的拉普拉斯矩阵的特征分解求U矩阵计算复杂；每一次前向传播，都要计算$U$,$diag(\theta_l )$及$U^T$三者的乘积，特别是对于大规模的graph，计算的代价较高，需要$\mathcal{O}(n^2)$的计算复杂度 （2）是非局部性连接的 （3）卷积核需要N个参数，当图中的节点N很大时是不可取的

于是第二个chebnet应运而生

Chebnet

chebnet

Hammond et al.(2011) ：Wavelets on graphs via spectral graph theory指出$g_θ(Λ)$可以很好的通过Chebyshev多项式$T_k(x)$的Kth-阶截断展开来拟合，并对$Λ$进行scale使其元素位于[−1,1]： $$ g_{\theta}(Λ)≈ \sum^{K}_{k=0}\theta_kT_k(\tilde{\Lambda}) $$ 其中：

  • $\tilde{\Lambda}=\frac{2\Lambda}{\lambda_{max}}-I_N$
  • $\lambda_{max}$为$L$的最大特征值，也叫谱半径
  • $\theta\in \mathbb{R}^K$是切比雪夫系数的向量
  • Chebyshev多项式递归定义$T_k(x) = 2xT_{k−1}(x) − T_{k−2}(x),其中T_0(x)=1,T_1(x)=x$

经过一系列的数学推导后:

$$ g_{\theta}\star x=\sum^K_{k=0}\theta_kT_k(\tilde{L})x $$ 类似的：$\tilde{L}=\frac{2L}{\lambda_{max}}-I_N$

GCN

GCN

GCN其实是在ChebNet的基础上使用一阶近似简化计算的方法得到的模型，即令K=1，$\lambda_{max}\approx2$: $$ g_{\theta'}\star x\approx \theta_{0}^{'}x+\theta_{1}^{'}(L-I_N)=\theta_{0}^{'}x-\theta_{1}^{'}D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x $$ 为了抑制参数数量防止过拟合，1stChebNet假设$\theta=\theta_{0}=-\theta_{1}$,为了解决数值不稳定和梯度爆炸、消失等问题引入一个trick：$$I_N+D^{−1/2}AD^{−1/2}\stackrel{\tilde{A=A+I_N}}{\longrightarrow} \tilde{D}^{−1/2}\tilde{A}\tilde{D}^{−1/2}$$

最后得到公式$Z=\tilde{D}^{−1/2}\tilde{A}\tilde{D}^{−1/2}X\Theta$，其中$\Theta$是滤波器的参数矩阵

书本章末尾说到：“As a simplification of spectral methods, the GCN model could also be regarded as a spatial method”

AGCN

自适应GCN学习隐含的点之间关系，其学习一个残差图拉普拉斯矩阵$L_{res}$，加入到原拉普拉斯矩阵中 $$ \widehat{L}=L+\alpha L_{res} $$ $$ L_{res}=I-\widehat{D}^{-\frac{1}{2}}\widehat{A}\widehat{D}^{-\frac{1}{2}} $$ $$ \widehat{D}=degree(\widehat{A}) $$

$\widehat{A}$通过一个以两个节点的特征为输入的可学习的距离函数来计算得来，idea源于认为图的欧式距离不适合图的结构信息，度量应该适应任务和输入的特征。

AGCN使用广义马氏距离$D(x_i,x_j)=\sqrt{(x_i-x_j)^TM(x_i-x_j)}$,其中$M$满足$M=W_dW_d^T$.

ACGN通过计算高斯核以及归一化高斯核G得到稠密邻接矩阵$\widehat{A}$

空域卷积

Neural FPs

$$ x=h^{t-1}_v+\sum_{i=1}^{|N_v|}{h^{t-1}_i} $$

$$ h_v^t=\sigma(xW_t^{|N_v|}) $$

其中：

  • $W_t^{N_v}$是第$t$层度为$|N_v|$的权重参数矩阵
  • $N_v$指节点$v$的邻居节点的集合
  • $h_v^t$是第$t$层节点$v$的嵌入层

通过公式我们可以看出，模型先把自己和邻居的嵌入向量加在一起，之后利用$W_t^{N_v}$转换。该模型给不同度数的节点定义了不同的$W_t^{N_v}$，这也导致该模型不能应用于大规模的图上。

PATCHY-SAN

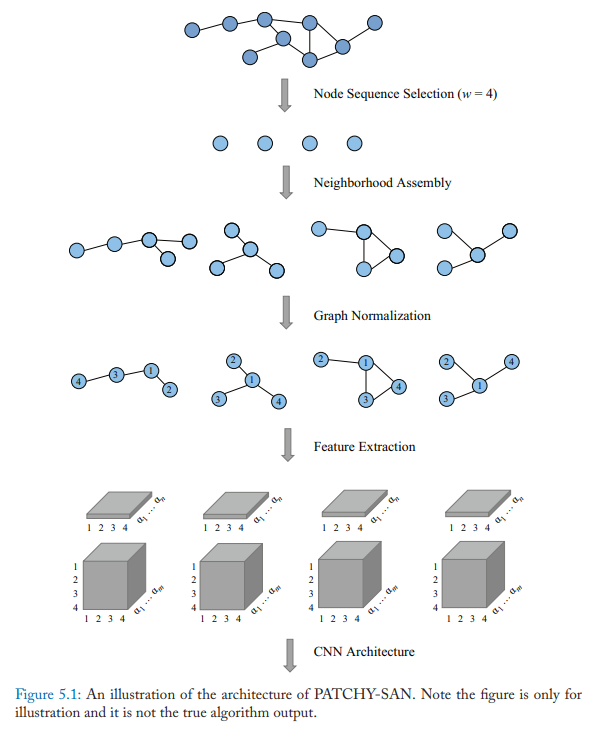
PATCHY-SAN

PATCHY-SAN模型首先选择并标准化k个邻居，然后用标准化邻域作为感受野，进行卷积运算。具体方法有四个步骤：

  1. 节点序列选择。即不选择所有的节点进行处理，而是首先使用图标记过程来获取节点的顺序并得到节点序列， 然后使用步长$s$从序列中选择节点，直到选择了$w$个节点
  2. 邻居聚合。每个节点的邻居作为候选，模型使用BFS搜索给每个节点选k个邻居节点。首先考虑一阶邻居，其次考虑高阶邻居。
  3. 图标准化。这一步的目的是给感受野中的节点一个顺序，便于把无序图空间映射到向量空间。
  4. 卷积结构。上一步感受野标准化后，就可以使用CNN结构啦。标准化的邻居作为感受野，节点和边的属性作为输入的channels。

DCNN

部分参考GNN模型：Diffusion-Convolutional Neural Networks - 知乎 (zhihu.com)

扩散卷积神经网络(DCNN)将图卷积看作一个扩散过程。它假设信息以一定的转移概率从一个节点转移到相邻的一个节点，使信息分布在几轮后达到均衡。

示意图

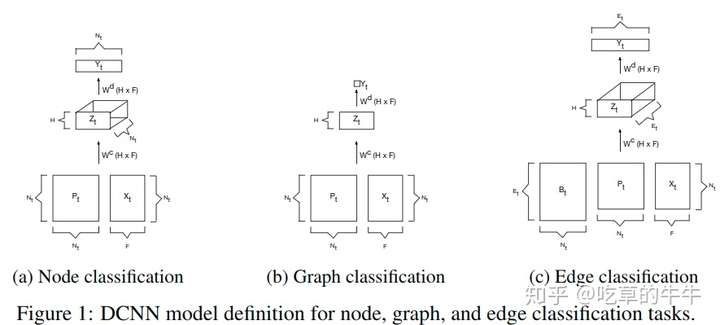
对于节点分类任务： $$ H=\sigma(W^c\odot P^*X) $$

  • $X$是输入向量 $(N\times F):N\rightarrow 节点数量,F\rightarrow特征数量$
  • $P^*$是矩阵$P$的power series，即${P,P^2,\dots,P^k}$,$(N\times K \times N)$
  • $P$是图邻接矩阵A的度归一化转移矩阵$(N\times N)$:
    • 对邻接矩阵A，将每一行中的每一个元素都除以对应行的和（也就是除以节点的度），相当于将对A的每一行进行了归一化处理，使得每一行的转移概率之和为1。
    • calculation:$P=D^{-1}A$
  • $\odot$是element-wise multiplication,即哈达玛积
  • $W^c$是$K\times F$的权重矩阵，$\sigma$为激活函数

我理解的整个计算过程含义是：输入一个维度为$F$,batch size为$N$的向量，通过一个$P^*$,$X(N\times F)\rightarrow P^*X(N\times K\times F)$。每个对象被转化成了定义在$K$跳$F$特征上的扩散卷积表示，再和权重矩阵对应位置相乘，激活后输出。最后$H$就是图中每个节点的扩散表示。

对于图分类任务，DCNN就简单地取每个节点的表示的平均值： $$ H=\sigma(W^c\odot 1^T_NP^*X/N) $$ $1^T_N$指$N\times 1$的全一向量

DGCN

DGCN

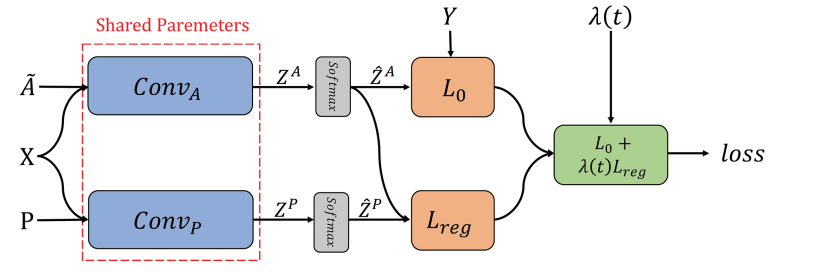
对偶图卷积网络（DGCN）共同考虑图的局部一致性和全局一致性。 它使用两个卷积网络来捕获局部/全局一致性，并采用无监督的损失函数对其进行集成。

第一个卷积网络与等式$Z=\tilde{D}^{−1/2}\tilde{A}\tilde{D}^{−1/2}X\Theta$ 相同, 第二个网络用正点向互信息（PPMI）矩阵替换邻接矩阵： $$ H^{'}=\sigma(D_P^{−1/2}X_PD_P^{−1/2}H\Theta) $$ 其中：

  • $X_P$是PPMI矩阵,$D_P$为$X_P$的对角度矩阵

该模型用第一个卷积网络考虑局部一致性，即相邻的节点有相似的标签，用第二个卷积网络考虑全局一致性，即认为有相似上下文邻居的节点有相似的标签。第一个和第二个卷积卷积分别记作$Conv_A$和$Conv_P$,再通过最终的损失函数集成这两个卷积： $$ L=L_0(Conv_A)+\lambda(t)L_{reg}(Conv_A,Conv_P) $$ 相关参数：

  • $L_0(Conv_A)$是已给节点标签的监督损失函数(交叉熵),假设有$c$个不同标签： $$ L_0(Conv_A)=-\frac{1}{|y_L|}\sum_{l\in y_L}\sum_{i=1}^cY_{l,i}ln(\widehat{Z}^A_{l,i}) $$

    • $Z_A$是$Conv_A$的输出函数
    • $\widehat{Z}^A$是$Z_A$经过softmax之后的输出
    • $y_L$是训练数据索引集,$Y$是真实标签

  • $\lambda(t)$是用来平衡两个损失函数的动态权重

  • $L_{reg(Conv_A,Conv_P)}$是用来衡量$\widehat{Z}^P$和$\widehat{Z}^A$之间差异的无监督损失函数

  • $ L_{reg(Conv_A,Conv_P)}=\frac{1}{n}\sum_{i=1}^n||\widehat{Z}^P_{i,:}-\widehat{Z}^A_{i,:}||^2 $

LGCN

可学习图卷积网络（LGCN）基于可学习卷积层（LGCL）以及子图训练策略。

LGCL使用CNN作为聚合器，它首先对节点的邻接矩阵做最大池化以获得top-k特征值，之后再使用一维CNN计算隐藏层表达。

即： $$ \widehat{H_t}=g(H_t,A,k) $$

$$ H_{t+1}=c(\widehat{H}_t), $$

  • A是邻接矩阵
  • $g(\cdot)$是选择k最大节点的操作
  • $c(\cdot)$是常规一阶CNN

对于每个节点，首先邻居的特征被搜集：假设某个节点有n个邻居，每个节点有c个特征，那么我们就获得了一个矩阵$M\in \mathbb{R}^{n\times c}$。如果n小于k，就用全0列填充。

对于每一列，我们选择最大k个值。最后在矩阵第一行加上节点本身的嵌入向量，变成$\widehat{M}\in \mathbb{R}^{(k+1)\times c}$

示意图如下：

LGCN

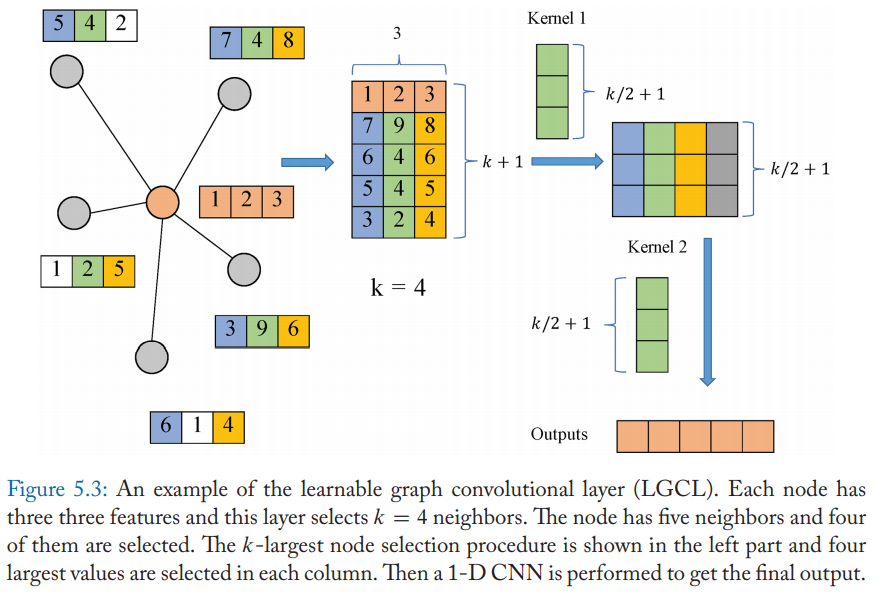
得到$\widehat{M}$后，用一维CNN将特征值聚合。

MoNet

Geodesic CNN(GCNN),Anisotropic CNN(ACNN),GCN和DCNN都可以看作是MoNet的实例。

用$x$表示图中的节点，$y\in N_x$表示$x$的邻居节点,MoNet计算节点和邻居之间的 $pseudo-coordinates$ $u(x,y)$,再在这些坐标中使用加权函数：

$$ D_j(x)f=\sum_{y \in N_x}w_j(u(x,y))f(y) $$

然后将非欧几里德域上的卷积的空间泛化定义为

$$ (f\star g)(x)=\sum^J_{j=1}g_iD_j(x)f $$

image-20210606091616520

GraphSAGE

参考GraphSAGE: GCN落地必读论文 - 知乎 (zhihu.com)

传播过程： $$ h^k_{N_v}=AGGREGATE_k(\{h^{k-1}_u,\forall u\in N_v\}) $$

$$ h_v^k=\sigma(W^k\cdot [h_v^{k-1}||h^k_{N_v}]) $$

image-20210620085229084

聚合函数：

  1. 归纳式聚合 $$ h_v^k=\sigma(W^k\cdot MEAN(\{h_v^{k-1}\}\cup \{h_u^{k-1},\forall u\in N_v\})) $$ Mean aggregator 和其他的aggregator不同，其没有拼接$h_v^{k-1}$和$h^k_{N_v}$,直接对目标节点和所有邻居embedding中每个维度取平均，之后再非线性转换

  2. 平均聚合 $$ h^k_{N(v)}=mean(\{h^{k-1}_u,\forall u\in N_v\}) $$

  3. LSTM聚合

    LSTM函数不符合“排序不变量”的性质，需要先对邻居随机排序，然后将随机的邻居序列embedding ${x_t,t\in N(v)}$作为LSTM输入

  4. Pooling聚合

    先对每个邻居节点上一层embedding进行非线性转换（等价单个全连接层，每一维度代表在某方面的表示（如信用情况）），再按维度应用 max/mean pooling，捕获邻居集上在某方面的突出的／综合的表现 以此表示目标节点embedding。 $$ h^k_{N(v)}=max(\{\sigma(W_{pool}h^k_{ui}+b),\forall u\in N_v\}) $$

损失函数：

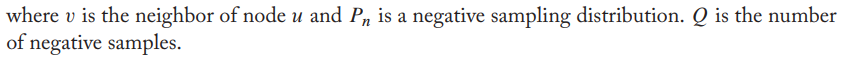
  1. 无监督损失函数 $$ J_G(z_u)=-log(\sigma(z_u^Tz_v))-Q\cdot E_{v_n~P_n(v)}log(\sigma(-z_u^Tz_{v_n})) $$ image-20210620093318207

  2. 有监督损失函数

    无监督损失函数的设定来学习节点embedding 可以供下游多个任务使用，若仅使用在特定某个任务上，则可以替代上述损失函数符合特定任务目标，如交叉熵。