PC-GNN理解与实现
PC-GNN 使用pick and choose 的方法解决的金融关系拓扑图中类别不平衡的问题,并且准确率达到SOTA.
希望理解了该篇论文,如有问题,欢迎指出。
另外感谢原作耐心的解答,感动
目录
解决问题
作者提出了两个角度的三个挑战分别是:
- 应用角度:一是关系上的冗余连接,与良好的实体的连接;二是缺少与欺诈节点直接连接(relation camouflage)
- 算法角度:GNN依赖于对邻居特征的聚合,类别数量不均衡会导致少数类特征被稀释
模型部分
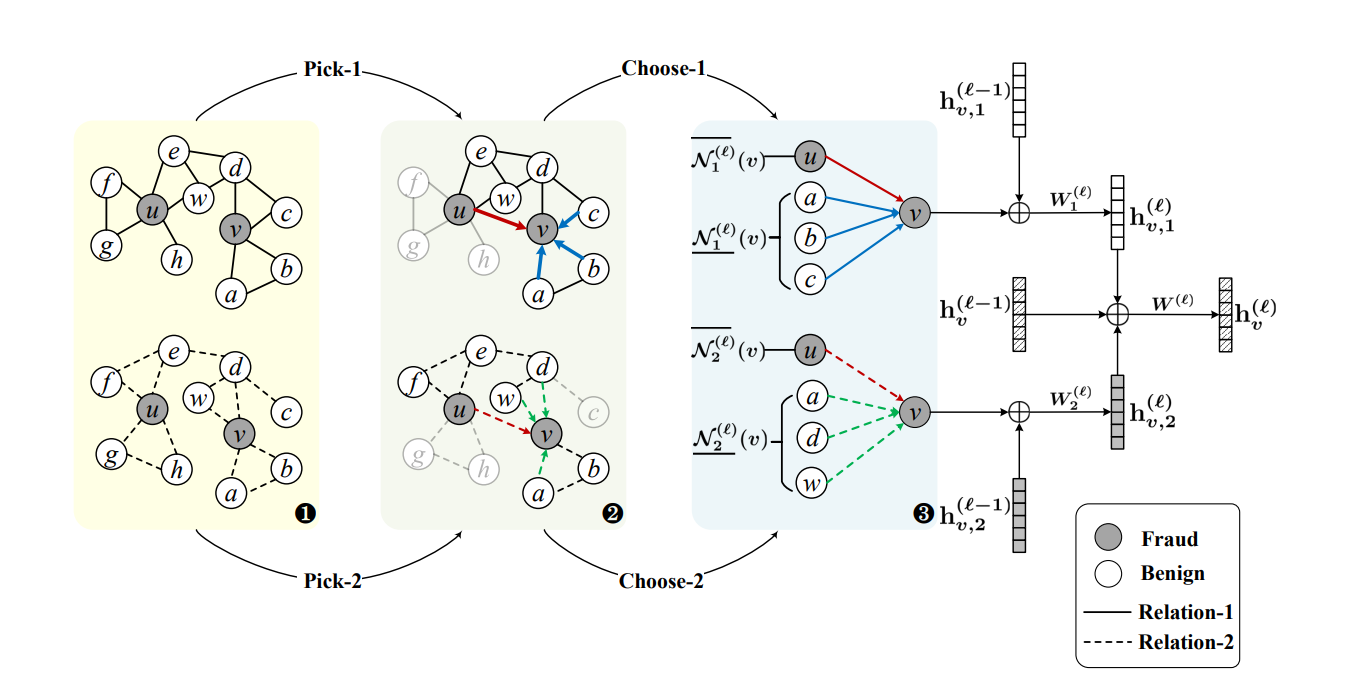
根据论文,模型主要分为pick、choose、aggregate三部分,分别针对节点的平衡采样、节点采样后得到图的对邻居节点的上采样和下采样、节点嵌入表达。
Pick
进行标签平衡采样,对图中节点进行采样,每个节点的采样概率为:
$$ P(v)\propto \frac{||\hat{A}(:,v)||^2}{LF(C(v))} $$ 其中:
- $\hat{A}$为所有关系的邻接矩阵之和的归一化,$\hat{A}=D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$,$A=\sum_{i=1}^RA_i$
- $LF(C(v))$为$v$对应的类别标签的频率
根据采样的公式可以发现,每个节点采样的概率和节点与其他节点的连接程度呈正比,和类别占比的多少呈反比,这样可以采样更多 邻居多且属于少数类别的节点,达到标签平衡采样的目的。
采样完的节点连同它们的一阶邻居构成新的子图。
但是这样就有了一个问题,根据上图,pick操作在一个epoch下应该是采样相同的节点,但图中显示有pick-1、pick-2两种不同的节点采样,推测原因是表示每个epoch中采样都不同。
Choose
对图上的标签进行平衡采样后,节点附近仍然存在冗余的相似邻居而缺少和欺骗节点直接的联系,不利于节点嵌入的学习,所以要进行节点邻居的选择。
对于属于多数类别的目标节点,只需下采样;对于少数类别的目标节点,同时进行上采样和下采样。
-
下采样 $$ \underline{\mathcal{N}_r^{l}(v)}={u\in \mathcal{V} |A_r(v,u)>0 and\ \mathcal{D}_r^l(v,u)<\rho _-} $$
-
上采样 $$ \overline{\mathcal{N}_r^{l}(v)}={u\in \mathcal{V} |C(u)=C(v) and\ \mathcal{D}_r^l(v,u)<\rho _+} $$
重点在于定义的距离函数,使用了L1范数衡量节点嵌入之间的距离: $$ \mathcal{D}_ r^ l (v,u)= ||D_r ^l (h_{v,r}^l)-D _r ^l(h_{u,r}^l) ||, $$
$$ D_r ^{l}(h_{v,r} ^l)=\sigma (U_r ^l h_{v,r} ^l) $$
先使用一个全连接层通过节点嵌入来预测节点属于诈骗节点的概率,再用L1范数得到两个节点之间的距离。
注意到有$l$,$r$,这意味着对于每层节点嵌入$l$的每个关系$r$,都要进行choose操作。
因为有一个全连接层用于端到端预测,所以需要一个损失函数来进行参数的学习,文中使用交叉熵损失函数,因为只需要判断是否为诈骗节点,即二分类:
$$ \mathcal{L}_{dist}=-\sum _{l=1} ^{L} \sum _{r=1} ^{R} \sum _{v\in \mathcal{V}} [y _{v} log p _{v,r}^l+(1-y_v) log(1-p _{v,r} ^l)] $$
$$ p_{v,r}^l=D_r^l(h_{v,r}^l) $$
Pick-Choose算法计算节点的嵌入表达:

Aggregate
思想是首先每次更新(即$l-1$层到$l$层MP过程),将每个关系下的得到的$l-1$层节点特征聚合得到各个关系的$l$层节点嵌入,之后再将所有关系下的$l$层部分节点嵌入以及$l-1$层的中心节点嵌入聚合在一起形成总的$l$层嵌入表达。
-
第一步获得各个关系下的$l$层嵌入: $$ h_{v,r}^l=Relu(W_r^l(h_{v,r}^{l-1}\oplus AGG_r^l\{{h_{u,r}^{l-1}\},u\in \mathcal{N}_r^l(v})) $$
,其中聚合器是平均聚合器。
-
第二步是获得总的$l$层嵌入表达: $$ h_{v}^l=Relu(W^l(h_{v}^{l-1}\oplus h_{v,1}^{l}\oplus \dots \oplus h_{v,R-1}^{l}\oplus h_{v,R}^{l})) $$
训练部分
这里作者选择使用MLP用于将节点嵌入转换为欺诈节点的预测概率:$$ \mathcal{L}_{gnn}=-\sum _{v\in \mathcal{V}} [y _{v} log p _{v,r}^l+(1-y_v) log(1-p _{v,r} ^l)], $$
其中$$ p_v=MLP(h_v^L) $$
总的损失函数为 $$ \mathcal{L} = \mathcal{L} _{gnn}+ \alpha \mathcal{L} _{dist} $$ 其中$\alpha$为平衡系数
实验部分
度量指标选择
macro-F1
micro-F1:
计算方法:先计算所有类别的总的Precision和Recall,然后计算出来的F1值即为micro-F1;
使用场景:在计算公式中考虑到了每个类别的数量,所以适用于数据分布不平衡的情况;但同时因为考虑到数据的数量,所以在数据极度不平衡的情况下,数量较多数量的类会较大的影响到F1的值;
marco-F1:
计算方法:将所有类别的Precision和Recall求平均,然后计算F1值作为macro-F1;
使用场景:没有考虑到数据的数量,所以会平等的看待每一类(因为每一类的precision和recall都在0-1之间),会相对受高precision和高recall类的影响较大;
AUC
AUC(Area Under Curve)被定义为ROC曲线(横坐标FPR,纵坐标TPR)下与坐标轴围成的面积,显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间。AUC越接近1.0,检测方法真实性越高;等于0.5时,则真实性最低,无应用价值。
GMean
$$ Gmean=\sqrt{TPR\cdot TNR} $$
值越大,表现越好。
实验参数设置
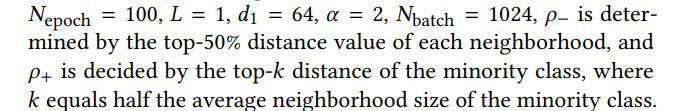
实验结果