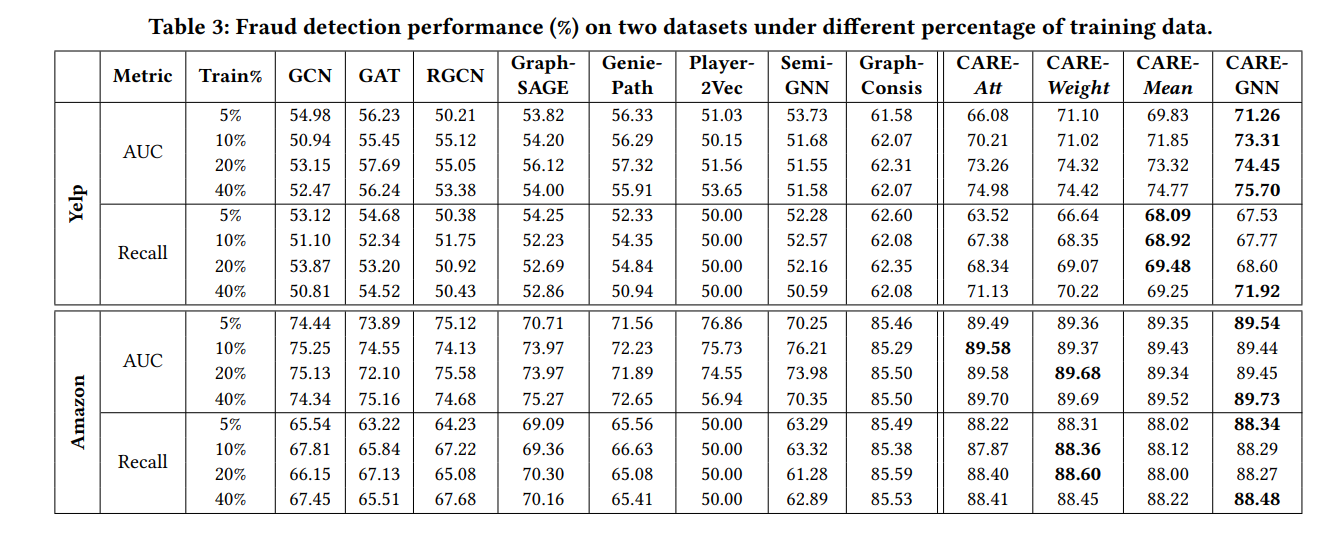
CARE-GNN分析理解及与PC-GNN的对比
PC-GNN之前发表的一篇解决识别伪装欺诈者(Graph Neural Network-based Fraud Detectors against Camouflaged Fraudsters)的图神经网络论文,PC-GNN也与之进行了对比。
解决问题
对比PC-GNN解决的是伪装欺诈者在图上的不平衡问题,CARE首先解决伪装欺诈者的端到端识别问题。
伪装欺诈者的伪装主要分为两部分
- Feature camouflage:聪明的骗子可能会调整他们的行为,在评论中添加特殊字符,或使用深度语言生成模型来掩盖明确的可疑结果,这些有助于绕过基于特征的检测器。
- Relation camouflage:骗子将自己与良好的实体关联在一起(比如定期发布评论或与有信誉的用户联系),以此逃避检测
伪装存在证明
根据作者github的更新:
| YelpChi | rur | rtr | rsr | homo |
|---|---|---|---|---|
| Avg. Feature Similarity | 0.991 | 0.988 | 0.988 | 0.988 |
| Avg. Label Similarity | 0.909 | 0.176 | 0.186 | 0.184 |
| Amazon | upu | usu | uvu | homo |
|---|---|---|---|---|
| Avg. Feature Similarity | 0.711 | 0.687 | 0.697 | 0.687 |
| Avg. Label Similarity | 0.167 | 0.056 | 0.053 | 0.072 |
- 对于特征伪装,计算节点特征向量的欧氏距离作为节点相似度,然后用全部的边的数量进行归一化,结果发现平均的节点相似度非常高。
- 对于关系伪装,基于两个相连的节点是否存在相同的标签来计算标签相似度,然后用全部的边的数量进行归一化。高标签相似度证明欺诈者未能成功伪装,而低标签相似度证明欺诈者成功伪装。结果只有R-U-R关系的标签相似度超过20%,其他均低于20%。
计算公式:

解决方法
于是,为了对抗骗子的伪装,作者提出三种手段:
- 针对特征伪装,提出标签感知相似度测量,基于节点特征来找到最相似的邻居。
- 针对关系伪装,设计了一个相似度感知邻居选择器,选择出一个关系中一个中心节点的相似的邻居。在GNN训练的过程中,使用强化学习找到最优的邻居选择阈值
- 使用学习到的邻居过滤阈值来规划一个关系感知邻居聚合器,将不同关系中的邻居节点信息结合在一起。
模型部分
标签感知相似度测量
无监督相似度度量手段难以将伪装的特征识别出来,所以需要一个有监督的参数化的相似度度量手段。
使用一层的MLP作为标签预测器,使用L1范式度量相似度
$$ \mathcal{D}^l(v,v^{'})=||\sigma(MLP^l(h_v^{l-1})-\sigma(MLP^l(h_{v^{'}}^{l-1})||_1 $$
$$ S^l(v,v^{'})=1-\mathcal{D}^l(v,v^{'}) $$
为了直接训练到标签的相似度度量参数,单独设置一个损失函数: $$ \mathcal{L}^l_{simi}=\sum_{v\in \mathcal{V}}-log(y_v \cdot \sigma(MLP^l(h_v^l))) $$
相似度感知邻居选择
Top-p Sampling:
对于第 $l$ 层关系 $r$ ,过滤的阈值为$p^l_r\in [0,1]$(闭区间说明可以全取或不取)
邻居个数选择$p^l_r\cdot | \{ S^l(v,v^{'}) \} |$,相似度降序排列
那么如何选择阈值$p^l_r$呢?
-
不存在梯度,也就没有办法使用BP训练更新
-
作者提出RL过程来选择最优超参
先计算一个epoch $e$内的平均距离: $$ G(\mathcal{D}^l_r)^e=\frac{\sum_{v\in V_{train}}\mathcal{D}^l_r(v,v^{'})^e}{|V_{train}|} $$ 使用强化学习的方法,奖赏定义为:两个epoch间,当平均距离减小时正值,平均距离增大时负值
$$ f(p_r^l,a_r^l)^e= \\ +1,G(\mathcal{D}_r^l)^{e-1}-G(\mathcal{D}_r^l)^{e}\ge 0 \\-1,G(\mathcal{D}_r^l)^{e-1}-G(\mathcal{D}_r^l)^{e}\lt 0 $$
终止条件为:
$$ |\sum^{e}_{e-10} f(p_{r}^{l},a_{r}^{l})^{e}|\le 2,where \ e\ge 10 $$
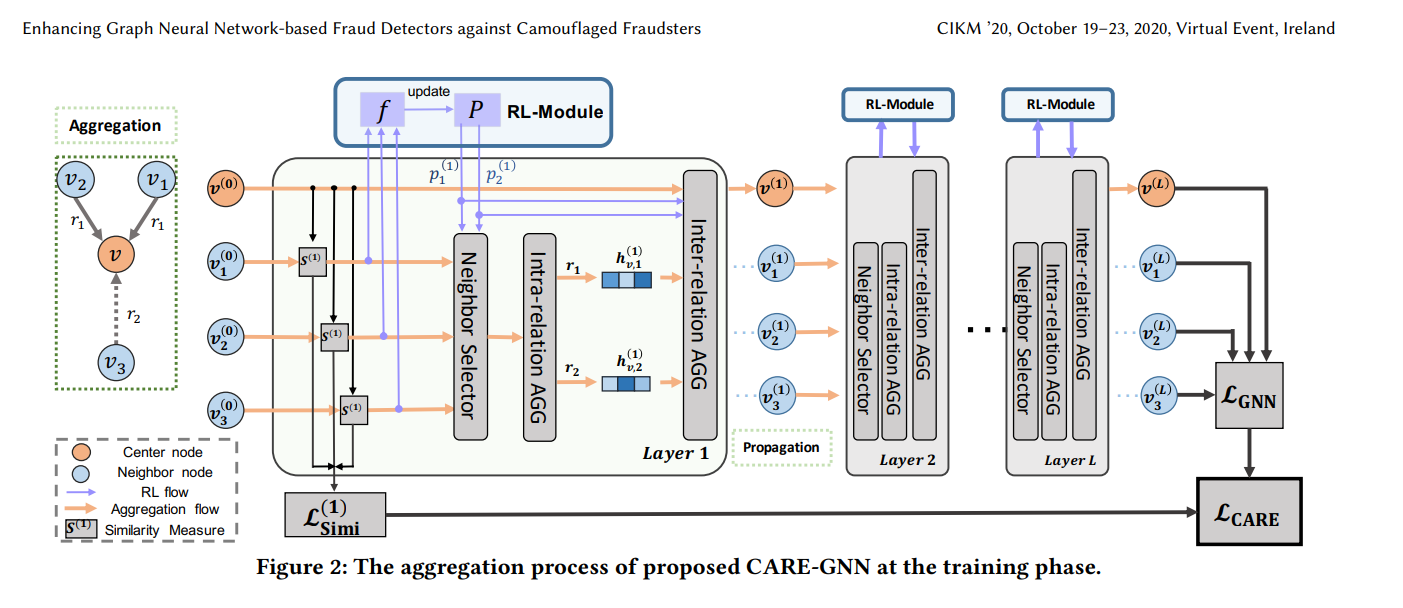
关系感知邻居聚合器
-
关系内聚合 $$ h^l_{v,r}=ReLU(AGG_r^l({h_{v^{'}}^{l-1}:(v,v^{'} )\in\mathcal{E}_r^l})) $$
-
关系间聚合 $$ h^l_{v,r}=ReLU(AGG_{all}^l(h_{v}^{l-1}\oplus{ p_r^l\cdot h_{v,r}^l}|_{r=1}^R)) $$
其中$p_r^l$是前面强化学习而来的参数,$AGG_{r}^l$是mean聚合器,
而$AGG_{all}$可以是任意种聚合器,作者在论文里测试了mean聚合器、Weight聚合器、attention聚合器、GNN聚合器。
损失函数: $$ \mathcal{L}_{GNN}=\sum_{v\in \mathcal{V}}-log(y_v\cdot \sigma(MLP(z_v))) $$ 其中使用MLP对节点嵌入进行二分类。
模型汇总
目标函数如下,综合了经验风险与结构风险,使用L2正则化以减少过拟合:

算法更新过程:

实验结果