近来在看对比学习，其中大量出现互信息的概念，和KL散度、交叉熵千丝万缕，加上总是记了又忘，所以觉得还是自己写个笔记比较好。

此文参考Visual Information Theory

目录

最优化编码

信息量用一个信息所需要的编码长度来定义,而一个信息的编码长度跟其出现的概率呈负相关,因为一个短编码的代价也是巨大的,因为会放弃所有以其为前缀的编码方式,比如字母”a”用单一个0作为编码的话,那么为了避免歧义,就不能有其他任何0开头的编码词了.所以一个词出现的越频繁,则其编码方式也就越短,同时付出的代价也大.

img

就像人们希望在经常使用的工具上投资更多一样，我们希望在经常使用的密码上花费更多。有一个特别自然的方法：将我们的预算与一个事件的常见程度成比例分配。因此，如果一个事件有50%的时间发生，我们就花50%的预算为它购买一个短码字。但是，如果一个事件只发生1%的时间，我们只花1%的预算，因为我们并不太关心这个密码是否很长。

计算熵

记得前面我们计算了长度为$L$的信息，代价为$\frac1{2^L}$,然后可以反过来得到这样一条公式$log_2(\frac1{cost})$

img

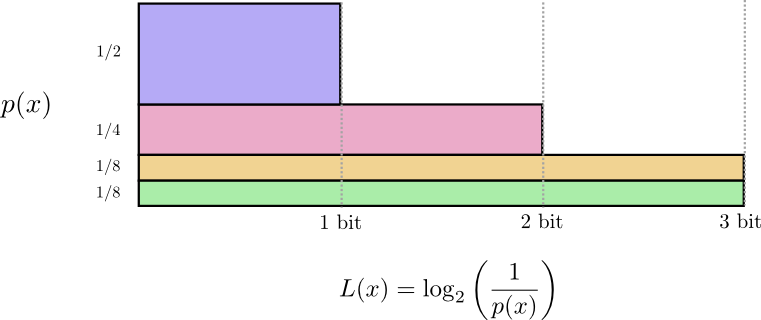
于是当我们知道了一个概率分布p之后，我们可以知道一个交流学习的平均最短的一个限制，其称为熵： $$ H(p) = \sum_x p(x)\log_2\left(\frac{1}{p(x)}\right)= - \sum p(x)\log_2(p(x)) $$ 无论我做什么，如果我想传达哪个事件发生，平均来说我至少需要发送这个数量的比特。

如果我确定会发生什么，我就根本不需要发送信息了!如果有两件事情以50%的概率发生，我只需要发送1比特。但是，如果有64种不同的事情以相同的概率发生，我就必须发送6比特。概率越集中，我就越能用简短的平均信息制作一个聪明的代码。概率越分散，我的信息就得越长。

结果越不确定，当我发现发生了什么时，平均来说我学到的东西就越多。

交叉熵

img

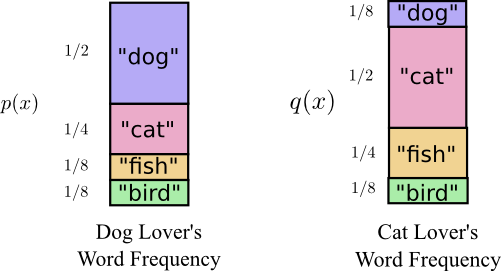
两者其实说的是相同的词汇，但是单词的频率发生了改变。

当我们使用一个分布的最优化编码来交流另一个分布中的事物时： $$ H_p(q) = \sum_x q(x)\log_2\left(\frac{1}{p(x)}\right) $$ 这称作交叉熵。

img

So, now we have four possibilities:

  • Bob using his own code $(H(p)=1.75 bits)$
  • Alice using Bob’s code $(Hp(q)=2.25 bits)$
  • Alice using her own code $(H(q)=1.75 bits)$
  • Bob using Alice’s code $(Hq(p)=2.375 bits)$

这告诉我们$H_p(q) \neq H_q(p)$

交叉熵给我们一种方法去衡量两个概率分布的不同程度。

KL散度

img

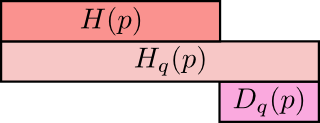
我们可以用一个具体的值来衡量熵与交叉熵的差距（即与最优化编码之间的距离）： $$ D_q(p) = H_q(p) - H(p)=\sum_x p(x)\log_2\left(\frac{p(x)}{q(x)} \right) $$ $D_q(p)$称为KL散度

直观的理解：p关于q的KL散度=p关于q的交叉熵-p的熵

有了KL散度和交叉熵，我们可以描述两个概率分布之间的差距，也就能够使得模型预测的分布接近于ground truth。

熵与多个变量

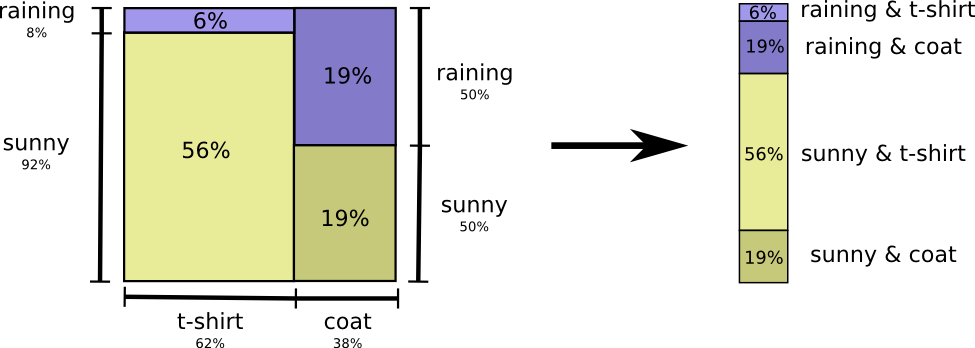
prob-2D-factored1-flat

对于多变量的概率分布，我们可以展开它，然后获得熵

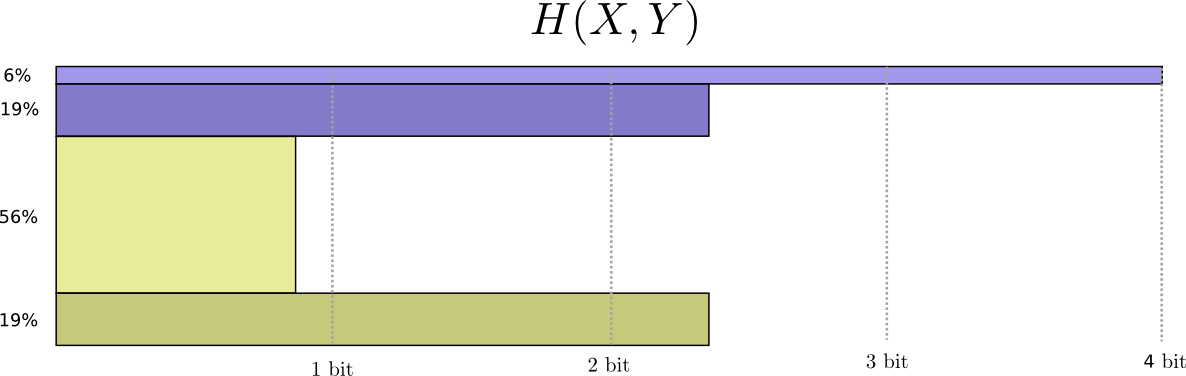
Hxy-flat

于是自然地定义$X$与$Y$的联合熵为： $$ H(X,Y) = \sum_{x,y} p(x,y) \log_2\left(\frac{1}{p(x,y)}\right) $$ 我们也可以用另一种方法看待联合熵，只是把代码长度看作一个第三维，现在，熵就是体积。

img

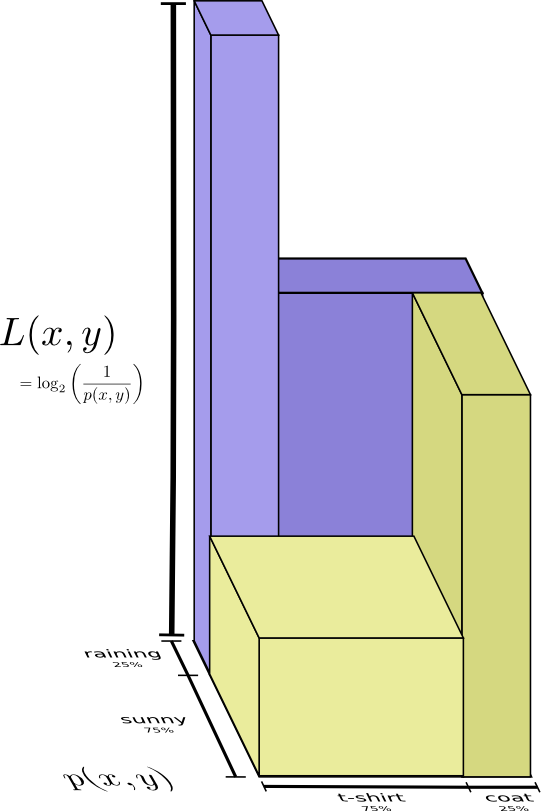
似乎我需要发送多少信息来传达我所穿的衣服。但实际上我需要发送更少的信息，因为天气强烈地暗示了我将穿什么衣服！我们分别考虑下雨和晴天的情况。让我们分别考虑下雨天和晴天的情况。

img

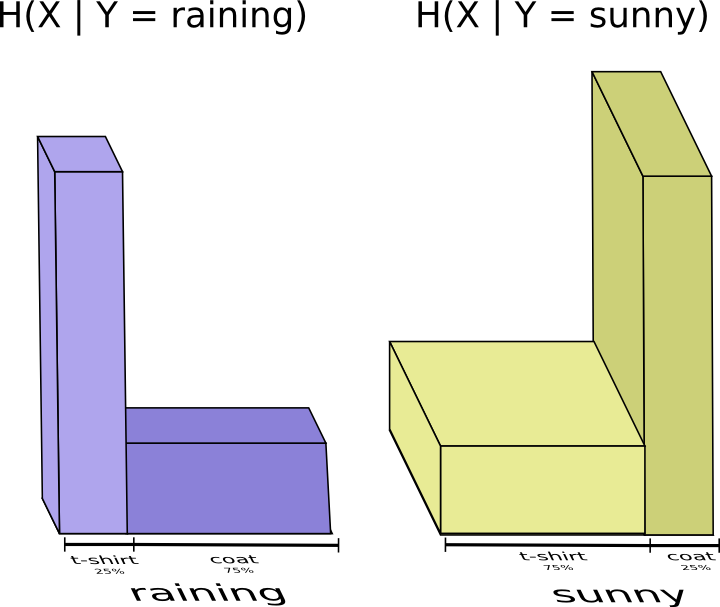
将上面二者放在一起计算

img

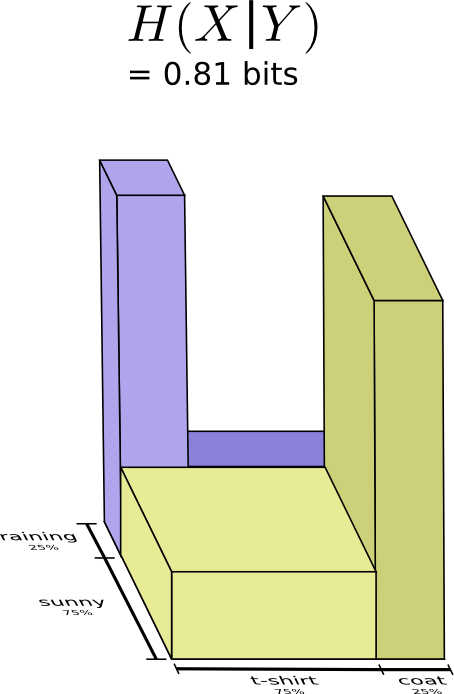
此时，我们称之为条件熵 $$ H(X|Y) = \sum_y p(y) \sum_x p(x|y) \log_2\left(\frac{1}{p(x|y)}\right) $$

互信息

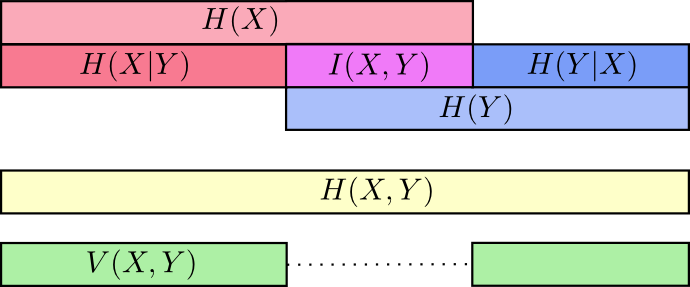
我们可以把信息看成条，熵和联合熵就可以这样描绘：

img

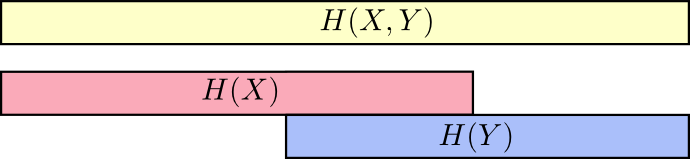
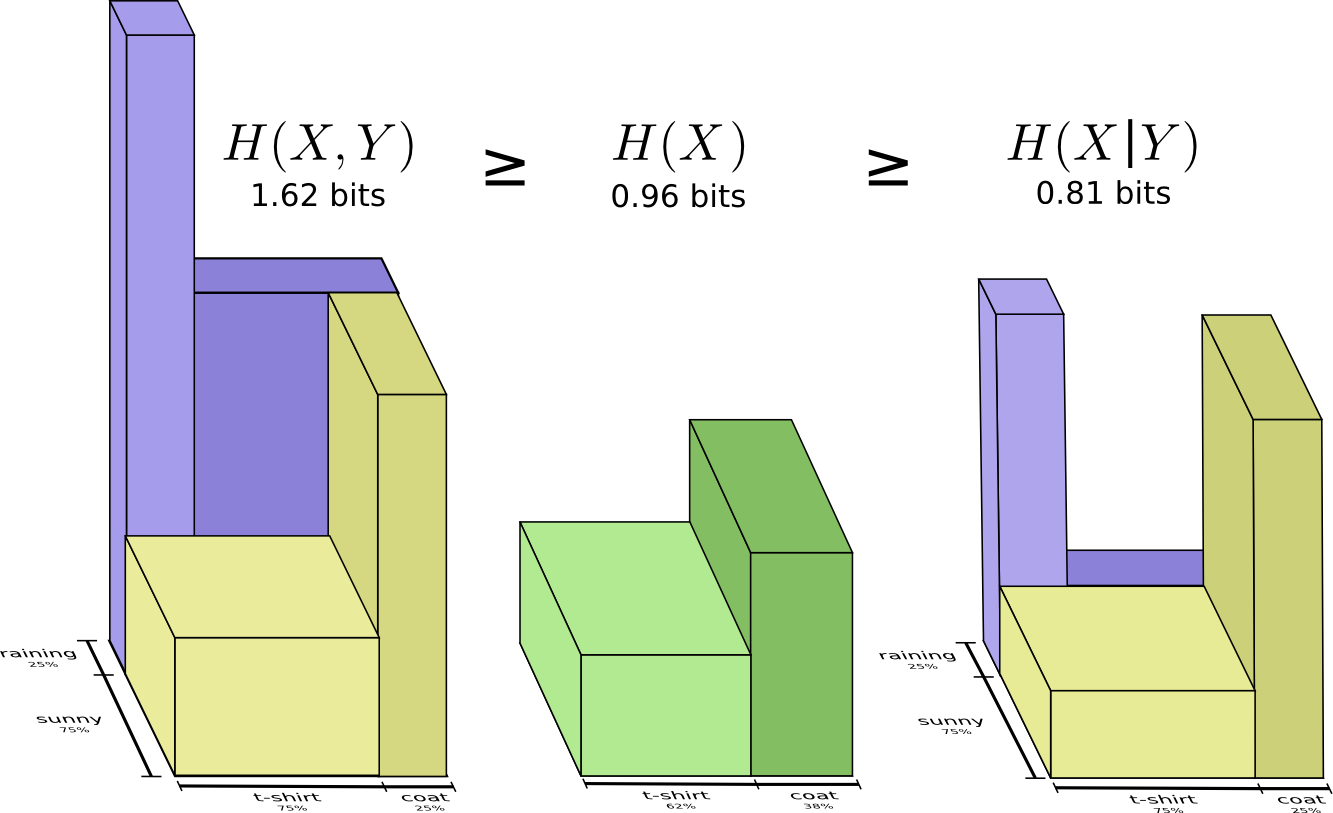
这样我们前面的说过的大小关系（沟通X和Y所需信息>沟通X所需信息>已知Y沟通X所需信息）就好理解了

img

所以$H(X|Y)$就是$H(X)$去掉与$H(Y)$重叠的部分

img

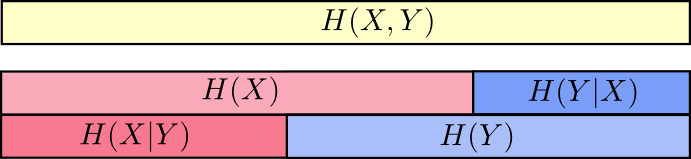
也很容易推出$H(X,Y) = H(Y) + H(X|Y)$

互信息定义为信息的交集 $$ I(X,Y) = H(X) + H(Y) - H(X,Y)= \sum_{x,y} p(x,y) \log_2\left(\frac{p(x,y)}{p(x)p(y)} \right) $$ 看起来和KL散度很像？

它就是KL散度！

它是$P(X,Y)$与其近似 $P(X)$ $P(Y)$ 间的KL散度，也就是说，如果你了解 $X$ 和 $Y$ 之间的关系，而不是假设它们是独立的，那么它代表 $X$ 和 $Y$ 所预计节省的比特数。

接着定义信息差异指标 $$ V(X,Y) = H(X,Y) - I(X,Y) $$ 它与KL散度之间的差别是：KL散度给我们提供了同一变量或变量集上两个分布之间的距离。与此相反，信息差异指标给我们提供了两个联合分布的变量之间的距离。KL散度是在分布之间，而信息差异指标是在一个分布之内。

img